AI/머신러닝
머신러닝의 이해와 라이브러리 활용 심화 1주차(EDA, 전처리, 인코딩, 스케일링, 데이터분리, 교차검증, GridSearch)
edcrfv458
2025. 2. 13. 15:39
목표
- 예측 모델링 프로세스
- 데이터 수집
- 탐색적 데이터 분석(EDA)
- 데이터 전처리
- (실습) 탐색적 데이터 분석과 데이터 전처리
- 데이터 분리
- (실습) 데이터 전체 프로세스 적용
- 데이터 분석 프로세스 정리
데이터 수집
- 데이터 수집 단계는 예제 데이터 혹은 회사에 있는 데이터로 진행되기 때문에, 지나치는 경우가 많다.
- 실제로 데이터를 수집하려면 개발을 통해 데이터를 적재하고 수집하는 데이터 엔지니어링 역량이 필요한데, 이 부분은 개발자가 직접 설계하고 저장하게 된다.
- 데이터 분석가는 이미 존재하는 데이터를 SQL 혹은 Python을 통해 추출하고 리포팅 혹은 머신러닝을 통한 예측을 담당한다고 할 수 있다.
용어
- Data Source
- OLTP Database: OnLine Transaction Processing 온라인 뱅킹, 쇼핑, 주문 입력 등 동시에 발생하는 다수의 트랜잭션(데이터베이스 직업의 단위) 처리 유형
- Enterprise Applications: 회사 내 데이터 (ex. 고객 관계 데이터, 제품 마케팅 세일즈)
- Third - Party: Google Analytics와 같은 외부소스에서 수집하는 데이터
- Web/Log: 사용자의 로그 데이터
- Data Lake: 원시 형태의 다양한 유형의 데이터 저장
- Data Warehouse: 보다 구조화된 형태로 정제된 데이터 저장
- Data Marts: 회사의 금융, 마케팅, 영업 부서와 같이 특정 조직의 목적을 위해 가공된 데이터
- Bl/Analytics business Intelligence(Bl): 의사결정에 사용될 데이터 수집하고 분석하는 프로세스
상황
- 회사 내 데이터가 존재
- SQL 혹은 Python 통해 데이터 마트 생성
- 회사 내 데이터가 존재 x ➡️ 데이터 수집이 필요
- CSV, EXCEL 파일 다운로드
- API를 이용
- Data Crawling
탐색적 데이터 분석(EDA)
- 데이터의 시각화, 기술통계 등의 방법을 통해 데이터 이해하고 탐구하는 과정이다.
- 이 과정에서 데이터에 대한 정보를 얻을 수도 있고, 적절한 모델링에 대한 정보도 얻을 수 있다.
- 예측 모델링이 아니더라도 데이터 분석에서는 반드시 필요한 과정이다.
- seaborn 라이브러리 활용
기술통계를 위한 EDA
- .describe()
- include='all' 옵션을 주면 범주형 데이터도 확인 가능
시각화 이용한 EDA
- countplot: 범주형 자료의 빈도 수 시각화
- 방법: 범주형 데이터의 각 카테고리 빈도수를 나타낼 때
- x축 범주형 자료
- y축 자료의 빈도수
- 예시: 각 날짜의 빈도수
- sns.countplot(x = 'day', data = tips)
- barplot: 범주형 데이터의 각 카테고리에 따른 수치 데이터의 평균을 비교
- x축 범주형 자료
- y축 연속형 자료
- 예시: 각 성별의 평균 소득을 비교할 때
- sns.barplot(x = 'sex', y = 'tip', data = tips)
- estimator: 어떻게 집계를 내릴지 결정하는 파라미터
- boxplot: 수치형 & 범주형 자료의 시각화
- 데이터의 분포, 중앙값, 사분위 수, 이상치 등을 한눈에 표현하고 싶을 때
- x축 수치형 or 범주형
- y축 수치형 자료
- 예시: 식사 시간 별 total_bill의 분포
- sns.boxplot(x = 'time', y = 'total_bill', data = tips)
- histogram: 수치형 자료 빈도 시각화 plt.hist or sns.histplot
- 연속형 분포 나타내고 싶을 때, 데이터가 몰려있는 구간을 파악하기 쉬움
- x축 수치형 자료
- y축 자료의 빈도수
- 예시: total_bill의 분포
- sns.histplot(x = 'total_bill', data = tips)
- bins: 막대의 개수 파라미터
- scatterplot: 수치형끼리 자료의 시각화
- 두 연속형 변수간의 관계를 시각적으로 파악하고 싶을 때
- x축 수치형 자료
- y축 수치형 자료
- 예시: total_bill과 tip 간 그래프를 산점도로 표현
- sns.scatterplot(x = 'total_bill', y = 'tip', data = tips)
- pairplot: 전체 변수에 대한 시각화
- 한 번에 여러 개의 변수를 동시에 시각화하고 싶을 때
- x축 수치형 or 범주형 자료
- y축 수치형 or 범주형 자료
- 대각선: 히스토그램
- sns.pairplot(tips)
데이터 전처리
- 전체 분석 프로세스에서 90%를 차지할 정도로 노동, 시간 집약적인 단계
이상치
- 관측된 데이터 범위에서 많이 벗어난 아주 작은 값 혹은 큰 값
- ESD 이용한 이상치 발견
- 데이터가 정규분포 따른다고 가정했을 때, 평균에서 표준편차의 3배 이상 떨어진 값
- 하지만 모든 데이터가 정규 분포를 따르지 않을 수 있기 때문에 다음 상황에서는 제한됨
- 데이터가 크게 비대칭일 때 (Log 변환을 이용해 볼 수 있음)
- 샘플 크기가 작을 경우
- IQR 이용한 이상치 발견
- ESD와 동일하게 비대칭이거나 샘플사이즈가 작은 경우 제한됨
- Box plot: 데이터의 사분위 수 포함하여 분포 보여주는 시각화 그래프
- 사분위 수: 데이터를 순서에 따라 4등분한 것
- 조건 필터링을 통한 삭제: df[df['column'] > limit_value]
# ESD 이상치 처리
import numpy as np
mean = np.mean(tips['total_bill'])
std = np.std(tips['total_bill'])
upper_limit = mean + 3*std
lower_limit = mean - 3*std
condition = (tips_df['total_bill'] > upper_limit)
tips[condition]
# IQR 이상치 처리
import seaborn as sns
sns.boxplot(tips['total_bill'])
q1 = df['column'].quantile(0.25)
q3 = df['column'].quantile(0.75)
IQR = q3 - q1
upper_limit = q3 + 1.5*IQR
lower_limit = q1 - 1.5*IQR
condition = (tips['total_bill'] > upper_limit)
tips[condition]- 이상치는 사실 주관적인 값이며 데이터 삭제 여부는 분석가가 결정해야 한다
- 이상치는 도메인과 비즈니스 맥락에 따라 그 기준이 달라지며, 데이터 삭제 시 품질은 좋아질 수 있지만 정보 손실을 동반하기 때문에 이상치 처리에 주의해야 한다
- 단지, 통계적 기준에 따라 결정 할 수 있다는 점만 기억
- 또한, Anomlay detection으로 데이터에서 패턴을 다르게 보이는 개체를 찾는 방법으로도 발전 가능하다
결측치
- 존재하지 않는 데이터
- 수치형 데이터 처리 방법
- 평균 값 대치: 대표적인 대치 방법
- 중앙 값 대치: 데이터에 이상치가 많아 평균 값이 대표성이 없다면 중앙 값 이용
- 범주형 데이터 처리 방법
- 최빈 값 대치
- 사용 함수
- 삭제 & 대치
- df.dropna(axis = 0) : 행 삭제
- df.dropna(axis = 1) : 열 삭제
- df.fillna(value) : 특정 값으로 대치 (평균, 중앙, 최빈값)
- 알고리즘 이용
- sklearn.impute.SimpleInputer : 평균, 중앙, 최빈값으로 대치
- SimpleImputer.statistics_ : 대치한 값 확인 가능
- sklearn.impute.IterativeImputer : 다변량대치(회귀 대치)
- sklearn.impute.KNNImputer : KNN 알고리즘을 이용한 대치
- sklearn.impute.SimpleInputer : 평균, 중앙, 최빈값으로 대치
- 삭제 & 대치
- isna() : 비어있는 값 확인
- notna() : 비어있지 않은 값 확인
# 행 제거
df.dropna(axis=0)
# 결측치 없는 행만 추출
cond = (df['Age'].notna())
df[cond]
# fillna 이용
age_mean = df['Age'].mean().round(2)
df['Age_mean'] = df['Age'].fillna(age_mean)
# SimpleImputer 이용
from sklearn.impute import SimpleImputer
si = SimpleImputer()
si.fit(df[['Age']])
si.statistics_ # 평균 값
df['Age_si_mean'] = si.transform(df[['Age']])- 대표적인 알고리즘 K-Nearest Neighbors(k 최근접 이웃)이라는 방법도 존재
범주형 데이터 전처리 - 인코딩
- 범주형 데이터에 적용!
- 어떤 정보를 정해진 규칙에 따라 변환하는 것
- 머신러닝 모델은 숫자를 기반으로 학습하기 때문에 반드시 인코딩 과정이 필요
크게 2가지로 나뉨
- 레이블 인코딩
- 정의: 문자열 범주형 값을 고유한 숫자로 할당
- 1등급 ➡️ 0
- 2등급 ➡️ 1
- 3등급 ➡️ 2
- 장점: 모델이 처리하기 쉬운 수치형으로 데이터 변환
- 단점: 실제로는 그렇지 않은데 순서 간 크기에 의미가 부여되어 모델이 잘못 해석할 수 있음
- sklearn.preprocessing.LabelEncoder
- 메소드
- fit: 데이터 학습
- transform: 정수형 데이터 변환
- fit_transform: fit과 transform 한 번에 실행
- inverse_transform: 인코딩된 데이터 원래 문자열로 반환
- 속성
- classes_: 인코더가 학습한 클래스(범주)
- 메소드
- 정의: 문자열 범주형 값을 고유한 숫자로 할당
- 원-핫 인코딩
- 정의: 각 범주를 이진 형식으로 변환하는 기법
- 빨강 ➡️ [1, 0, 0]
- 파랑 ➡️ [0, 1, 0]
- 초록 ➡️ [0, 0, 1]
- 명목형 데이터에 권장
- 장점: 각 범주가 독립적으로 표현되어 순서가 중요도를 잘못 학습하는 것을 방지
- 단점: 범주 개수가 많을 경우 차원이 크게 증가, 모델의 복잡도가 증가, 과적합 유발
- 사용 함수
- 1. pd.get_dummies: 더미화
- 2. sklearn.preprocessing.OneHotEncoder
- 메소드는 LabelEncoder와 동일
- categories_: 인코더가 학습한 클래스(범주)
- 정의: 각 범주를 이진 형식으로 변환하는 기법
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
le = LabelEncoder()
oe = OneHotEncoder()
# 성별은 LabelEncoder
le.fit(df[['sex']])
le.classes_
df['sex_le'] = le.transform(df[['sex']])
# 항구는 OneHotEncoder
oe.fit(df[['embarked']])
oe.categories_
embarked_csr = oe.transform(df[['embarked']]) # 차원이 엄청나게 큼
embarked_csr_df = pd.DataFrame(embarked_csr.toarray(), columns=oe.get_feature_names_out()) # toaaray로 쭉 피고, 컬럼 목록 가져와 데이터프레임 화 시킴
pd.concat([df, embarked_csr_df], axis=1)수치형 데이터 전처리 - 스케일링
- 수치형 데이터에 적용!
- 머신러닝 학습에 사용되는 데이터들은 서로 단위 값이 다르므로 보정하는 것
이론적으로 3가지가 있지만 2개를 주로 사용
- 표준화(Standardization)
- 각 데이터에 평균을 빼고 표준편차를 나누어 평균을 0, 표준편차를 1로 조정하는 방법
- 함수: sklearn.preprocessing.StandardScaler
- 메소드
- fit: 데이터 학습(평균과 표준편차 계산)
- transform: 데이터 스케일링 진행
- 속성
- mean_: 데이터의 평균값
- scaler_, var_: 데이터의 표준 편차, 분산값
- n_features_in_: fit 할때 들어간 변수의 개수
- feature_names_in_: fit 할 때 들어간 변수 이름
- n_samples_seen_: fit 할때 들어간 데이터의 개수
- 메소드
- 장점
- 이상치가 있거나 분포가 치우쳐져 있을 때 유용
- 모든 특성의 스케일을 동일하게 맞춤
- 단점
- 데이터의 최소/최대 값이 정해져있지 않음
- 정규화(Normalization)
- 데이터를 0과 1사이 값으로 조정
- 함수: sklearn.preprocessing.StandardScaler
- 속성
- data_min_: 원 데이터의 최소 값
- data_max_: 원 데이터의 최대 값
- data_range_: 원 데이터의 최대-최소 범위
- 속성
- 장점
- 이상치가 없을 때 유용
- 모든 특성의 스케일을 동일하게 맞춤
- 최대-최소 범위가 명확
- 단점
- 이상치에 영향을 많이 받을 수 있음
- 로버스트 스케일링(Robust Scaling)
- 중앙값과 IQR을 사용하여 스케일링
- 함수: sklearn.preprocessing.RobustScaler
- 속성
- center_: 훈련데이터의 중앙값
- 속성
- 장점
- 이상치의 영향에 덜 민감
- 단점
- 표준화와 정규화에 비해 덜 사용됨
실습 (age는 MinMaxScaler, fare는 StandardScaler 적용)

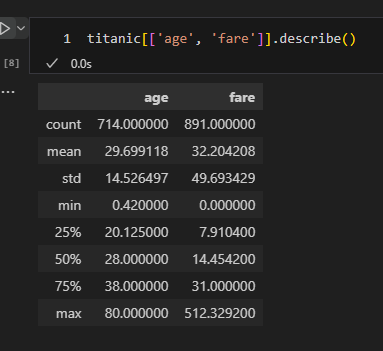
from sklearn.preprocessing import MinMaxScaler, StandardScaler
mm_sc = MinMaxScaler()
sd_sc = StandardScaler()
titanic['age_mm_sc'] = mm_sc.fit_transform(titanic[['age']])
titanic['fare_sd_sc'] = sd_sc.fit_transform(titanic[['fare']])
titanic.head(3)데이터 분리
과적합
- 데이터를 너무 과하게 학습해서 해당 문제만 잘 맞추고 새로운 데이터에 대해서는 잘 맞추지 못하는 현상
예측 혹은 분류를 하기 위해 모델 복잡도를 설정
- 모델이 지나치게 복잡할 때: 과대적합 발생 가능성 존재
- 모델이 지나치게 단순할 때: 과소적합 발생 가능성 존재
원인
- 모델의 복잡도
- 데이터 양이 충분하지 않은 경우
- 학습 반복이 많은 경우(딥러닝)
- 데이터 불균형의 경우
해결법 - 테스트 데이터의 분리
- 함수: sklearn.model_selection.train_test_split
- 파라미터:
- test_size: 테스트 데이터 세트 크기
- train_size: 학습 데이터 세트 크기
- shuffle: 데이터 분리 시 섞기
- random_state: 동일한 데이터로 분리하기 위한 난수 값, 실행시킬 때마다 같은 데이터로 분리됨
- stratify: 예를 들어 label이 0, 1의 비율이 8:2 일 때 그냥 split을 하게 되면 0이 많이 뽑힐 수도 있다. 하지만 stratify=y를 주게 되면 원본 데이터의 label의 비율을 이용해 split된 데이터의 label의 비율도 맞춰준다.
- 반환 값:
- X_train, X_test, y_train, y_test
- 파라미터:
실습 - x: fare, sex, y:survived
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(titanic[['fare', 'sex']], titanic['survived'],
test_size=0.3, shuffle=True, random_state=42, stratify=y)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)실습: 데이터 전체 프로세스 적용
- 데이터 로드 & 분리 ➡️ train / test
- 탐색적 데이터 분석(EDA) ➡️ 분포 & 이상치
- 데이터 전처리
- 결측치: 수치형 / 범주형 / 삭제
- 전처리: 수치형 / 범주형(레이블 인코딩, 원-핫 인코딩)
- 모델 수립
- 평가
교차 검증과 GridSearch
- 위에서 모델을 평가하기 위해 별도의 테스트 데이터로 평가하는 과정을 알아봄
- 하지만, 고정된 테스트 데이터가 존재하기 때문에 과적합에 취약한 단점
교차 검증
- 데이터 셋을 여러 개의 하위 집합으로 나누어 돌아가면서 검증 데이터로 사용하는 방법
K-Fold Validation
- Train Data를 K개의 하위 집합으로 나누어 모델 학습시키고 모델을 최적화하는 방법
- K는 분할의 개수
- 특징: 데이터가 부족할 경우에 유용(반복 학습)
- 함수
- sklearn.model_selection.KFold
- sklearn.model_selection.StrifiedKFold: 불균형한 레이블 가지고 있을 때 사용
from sklearn.model_selection import KFold
kfold = KFold(n_splits = 5)
scores = []
X = train_df_2[['Age_mm_sc', 'Fare_sd_sc', 'Family_mm_sc', 'Pclass_le', 'Sex_le', 'Embarked']]
y = train_df_2['Survived']
for i, (train_index, test_index) in enumerate(kfold.split(X)):
X_train, X_test = X.values[train_index], X.values[test_index]
y_train, y_test = y.values[train_index], y.values[test_index]
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
model_lor2 = LogisticRegression()
model_lor2.fit(X_train, y_train)
y_pred2 = model_lor2.predict(X_test)
accuracy = accuracy_score(y_test, y_pred2).round(3)
print(i, '번째 교차검증 정확도는', accuracy)
scores.append(acuuracy)
print("평균 정확도", np.mean(scores))
하이퍼 파라미터 자동 적용하기 - GridSearch
- 하이퍼 파라미터: 사람이 정해줘야 하는 모델의 입력 값
- GridSearch: 다양한 값을 넣고 실험하는 것을 자동화해주는 것
from sklearn.model_selection import GridSearchCV
params = {'solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'],
'max_iter': [100, 200]}
grid_lor = GridSearchCV(model_lor2, param_grid = params, scoring = 'accuracy', cv = 5)
grid_lor.fit(X_train, y_train)
print("최고의 파라미터", grid_lor.best_params_)
print("최고의 정확도", grid_lor.best_score_.round(3))